M-Star Path Algorithm
The M-Star (M*) Path Algorithm is a Patent Protected Algorithm that is aimed at finding a route
between two points in a graph or grid without exploration of the entire domain.
In its basic form, the algorithm makes use of a matrix that defines the grid (usually in 2D but can equally be used in 3D or even n-D)
through a parametric representation of all the nodes and connections.
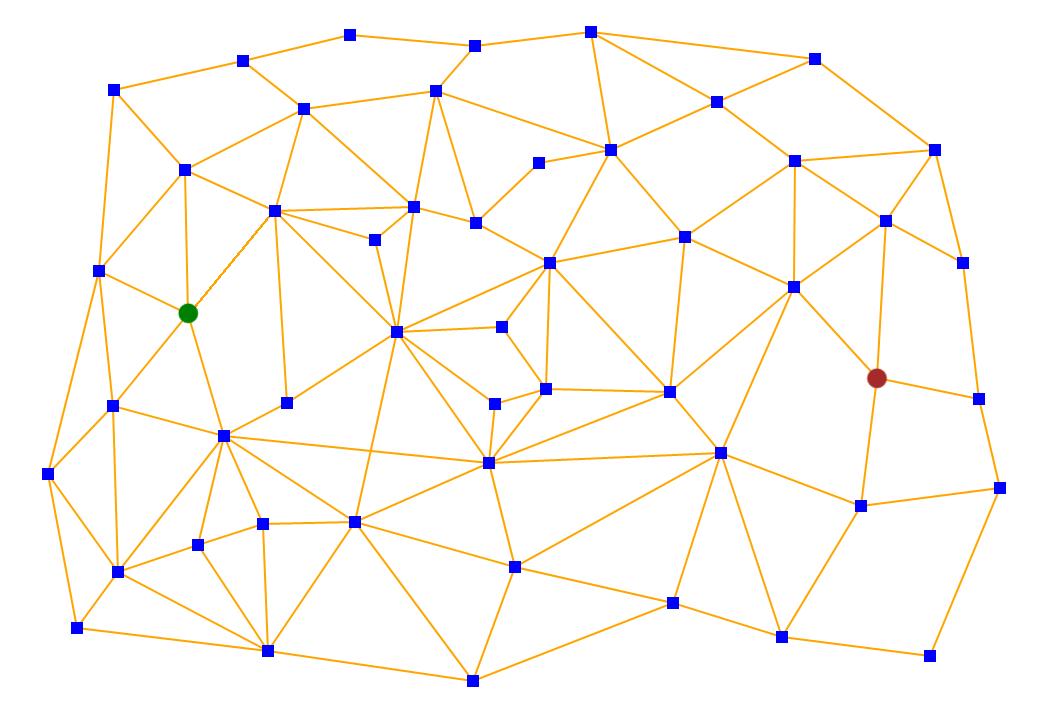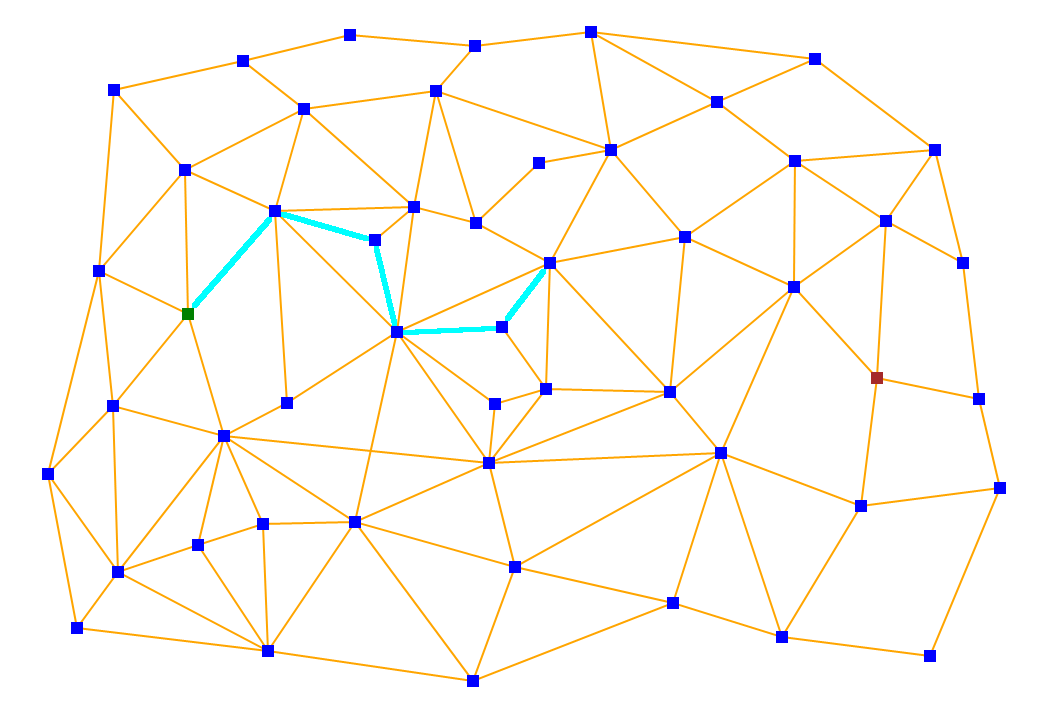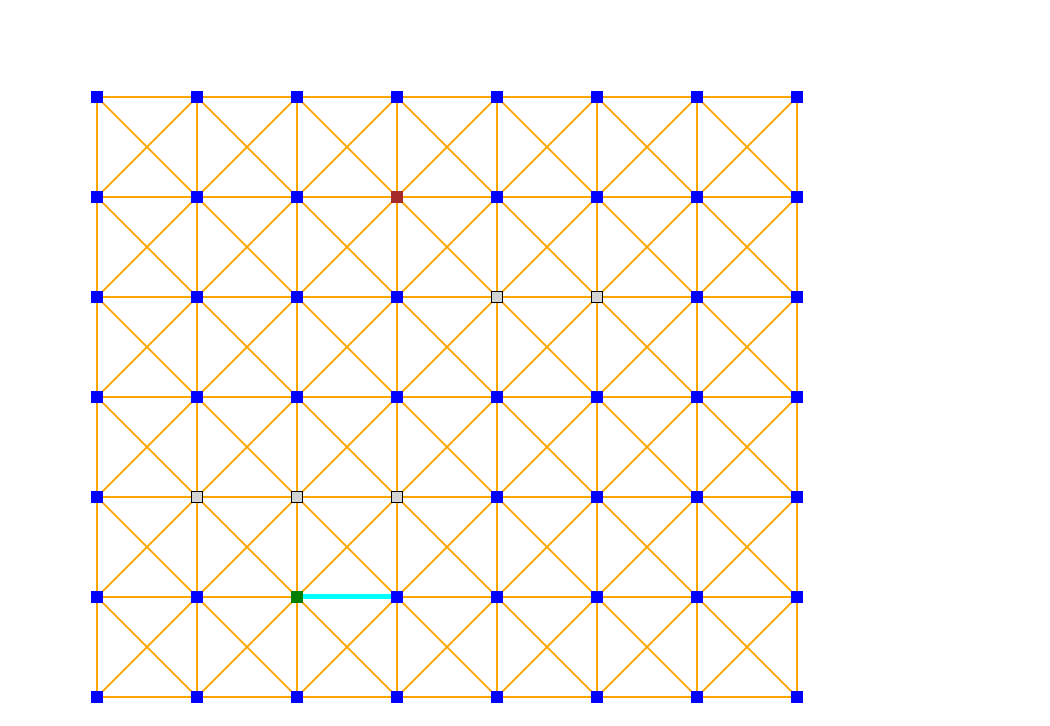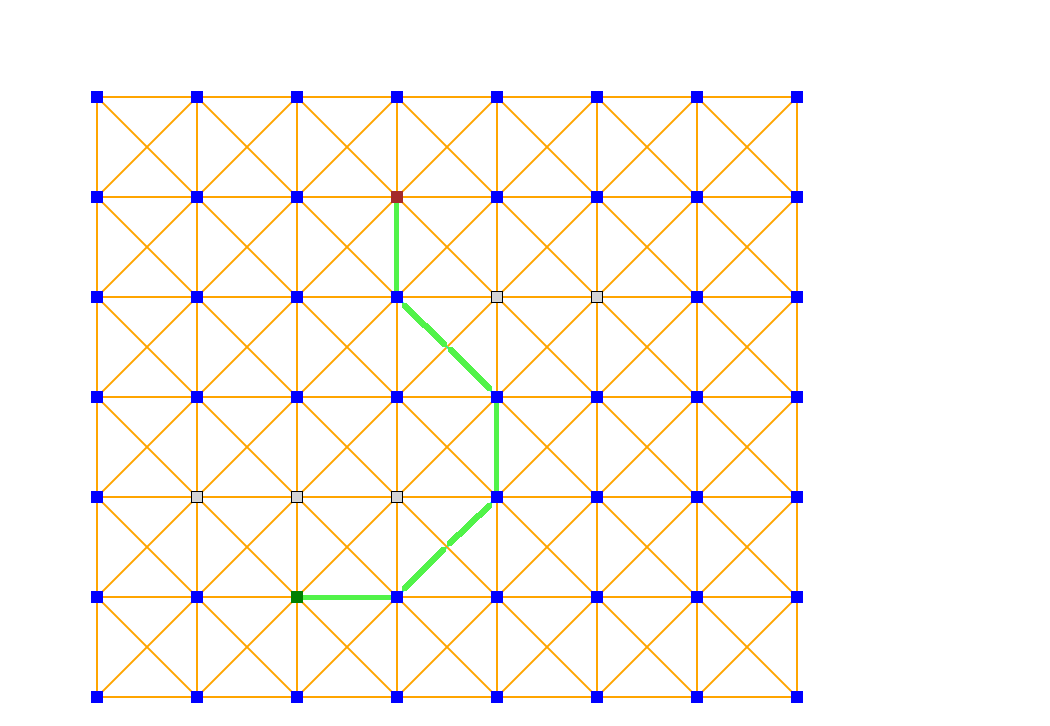
The path between the two points is a property of the matrix and as such only a single segment (i.e. the next node in the path) can be computed -or the entire path- depending on the situation at hand.
Since the matrix is dependent only on the grid being used, it can be pre-calculated and stored without requiring an update when the two points are modified.
Further use of the Algorithm includes it use in Obstacle Avoidance (where 'No-Go' regions may be dynamically added or removed without re-computation of the grid) and in Social Grids (where the shortest distance is less of a concern rather than whether two points are connected at all).
In general, the M* Path Algorithm (once the grid has been defined) achieves a time complexity as low as O(S*C) (where S is the number of steps that it takes to connect the points and C is the average number of connections at each of those steps). Determination of the 'next' step from a current location towards a destination has thus a complexity of O(C).
The purpose of this site is to provide information to interested parties.
Currently, the algorithm has been implemented into development libraries and the focus is on finding a partner to support further work or an interested party to license/purchase the algorithm for further commercial development and implementation.
At this time, only invited users may access the details and overview. If you are interested in this algorithm for commercial use, please use the Contact page to get in touch and request further information.
Note: this site is best viewed in FireFox 45 or Internet Explorer 11
|
|
|